Arrival theorem

In queueing theory, a discipline within the mathematical theory of probability, the arrival theorem[1] (also referred to as the random observer property, ROP or job observer property[2]) states the state of a system immediately before an arrival is independent of that arrival.[3] In other words, the distribution a customer in transit to state i 'see's is the equilibrium distribution of the system.

The arrival theorem always holds in open product form networks with unbounded queues at each node, but it also holds in more general networks. A necessary and sufficient condition for the arrival theorem to be satisfied in product form networks is given in terms of Palm probabilities in Boucherie & Dijk, 1997.[4] A similar result also holds in some closed networks. An example of a product form network where the arrival theorem does not hold is reversible Kingman networks.[4][5]

Contents

Theorem for arrivals governed by a Poisson process

For Poisson processes the property is often referred to as the PASTA property (Poisson Arrivals See Time Averages) and states that the probability of the state as seen by an outside random observer is the same as the probability of the state seen by an arriving customer.[6] The property also holds for the case of a doubly stochastic Poisson process where the rate parameter is allowed to vary depending on the state.[7]

Theorem for Jackson networks

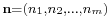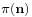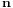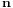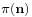In an open Jackson network with m queues, write \scriptstyle{\mathbf{n} = (n_1, n_2, \ldots, n_m)} for the state of the network. Suppose \scriptstyle{\pi(\mathbf{n})} is the equilibrium probability that the network is in state \scriptstyle{\mathbf{n}}. Then the probability that the network is in state \scriptstyle{\mathbf{n}} immediately before an arrival to any node is also \scriptstyle{\pi(\mathbf{n})}.

Note that this theorem does not follow from Jackson's theorem, where the steady state in continuous time is considered. Here we are concerned with particular points in time, namely arrival times.[8] This theorem first published by Sevcik and Mitrani in 1981.[9]

Theorem for Gordon–Newell networks

In a closed Gordon–Newell network with m queues, write 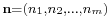\scriptstyle{\mathbf{n} = (n_1, n_2, \ldots, n_m)} for the state of the network. For a customer in transit to state i, let 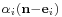\scriptstyle{\alpha_i(\mathbf{n}-\mathbf{e}_i)} denote the probability that immediately before arrival the customer 'sees' the state of the system to be

\mathbf{n}-\mathbf{e}_i = (n_1,n_2,\ldots,n_i - 1,\ldots,n_m).\,

This probability, 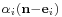\scriptstyle{\alpha_i(\mathbf{n}-\mathbf{e}_i)}, is the same as the steady state probability for state 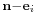\scriptstyle{\mathbf{n}-\mathbf{e}_i} for a network of the same type with one customer less.[10]

Notes

  1. ^ Asmussen, Søren (2003). Applied Probability and Queues. Springer. p. 134. ISBN 0387002111. 
  2. ^ El-Taha, Muhammad (1999). Sample-path Analysis of Queueing Systems. Springer. p. 94. ISBN 0792382102. 
  3. ^ Mitrani, Isi (1987). Modelling of computer and communication systems. Cambridge computer science texts. p. 47. ISBN 0521314224. 
  4. ^ a b Boucherie, Richard J.; Dijk, Nico M. (1997). "On the arrival theorem for product form queueing networks with blocking". Performance Evaluation (Elsevier) 29: 155–176. doi:10.1016/S0166-5316(96)00045-4. 
  5. ^ Kingman, J. F. C. (1969). "Markov Population Processes". Journal of Applied Probability (Appled Probability Trust) 6 (1): 1–18. doi:10.2307/3212273. JSTOR 3212273. 
  6. ^ Wolff, Ronald W. (1982). "Poisson Arrivals See Time Averages". Operations Research 30 (2): 223–231. doi:10.1287/opre.30.2.223. JSTOR 170165. 
  7. ^ van Doorn, Erik A; Regterschot, G.J.K (October 1988). "Conditional PASTA". Operations Research Letters 7 (5): 229–232. doi:10.1016/0167-6377(88)90036-3. http://doc.utwente.nl/70043/1/Doorn88conditional.pdf. 
  8. ^ Harrison, Peter G.; Patel, Naresh M. (1992). Performance Modelling of Communication Networks and Computer Architectures. Addison-Wesley. p. 228. ISBN 0201544199. 
  9. ^ Sevcik, K.C.; Mitrani, Isi (1981). "The distribution of queueing network states at input and output instants". J. ACM 28 (2): 358–371. doi:10.1145/322248.322257. 
  10. ^ Breuer, Lothar; Baum, D (2005). An Introduction to Queueing Theory and Matrix-analytic Methods: And Matrix-Analytic Methods. Springer. p. 93. ISBN 1402036302.